1. Introduction
Many students struggle with introductory algebra and teachers have little to guide them in assisting students to learn this important component of high school mathematics. Little is known about the effect of students’ numeracy on the learning of early algebra, or about the strategies that students use to solve equations.
There is widespread agreement that algebra is not easily understood by many students. The Cockcroft Report in the United Kingdom highlighted the fact that algebra is a source of considerable confusion and negative attitudes among pupils (Cockcroft, 1982), while the title of Brekke’s (2001) paper, “School Algebra: Primarily Manipulations of Empty Symbols on a Piece of Paper?”, sums up the situation for many students.
Thomas and Tall (2001) describe the long-term cognitive development of symbolic algebra as moving from the processes and mathematical objects of arithmetic, to evaluation processes in generalised arithmetic, to manipulation of mathematical objects in manipulation algebra, and finally to defined concepts in axiomatic algebra. They suggest that each transition involves considerable cognitive reconstruction that acts as a barrier for many. Bednarz, Kieran, and Lee (1996) comment that algebra in schools is often reduced to rules for transforming and solving equations. As rule-based algebra can be regarded as axiomatic, it is not surprising that so many students experience confusion when a rule-based approach is used.
Because much arithmetic in schools is presented as a computation ready to complete (for example, 3 + 5 = ) and because pressing the equals button on a calculator performs a calculation on whatever has been entered, children understand “equals” as meaning compute now rather than is equivalent to (Booker, 1987; Booth, 1988). Linchevski (1995) states that in the transition from arithmetic to algebra, children need to move from a unidirectional view of the equals sign to a multidirectional one. Closely related to this is the use of an equation as a process, rather than an object that can be operated on (Sfard, 1991). Children initially see equations as the description of an arithmetic process (for example, 2 x 3 + 4 = x), and when presented with an equation to solve (for example, 2x + 4 = 10), they also see it as the description of an arithmetic process with guess and check as a natural way of finding x.
Children’s stage of numeracy is likely to be important for their understanding of expressions and equations (Irwin, 2002). Equations of the form x + 3 = 7 can be solved by advanced counters (Ministry of Education, 2003b) by guess and check, but can be solved much more easily by “part–whole”[1] thinkers (Ministry of Education, 2003b) able to visualise 7 as 3 + 4. It can be argued that to solve equations such as 3x = 15 requires multiplicative part–whole thinking if a child is to do more than simply follow prescribed algorithms. Furthermore, equations of the kind 2x + 3 = 11 might require an understanding of numbers beyond simple additive part–whole or multiplicative part–whole thinking. Linear equations derived from relatively simple situations can be complex and require an understanding of the use of brackets; the hierarchy of operations; the commutative, associative, and distributive laws; and how to use inverse operations (Fairchild, 2001).
A recent doctoral study by Linsell (2005b) investigated the development of algebraic thinking in a group of four Year 9 students. Learning to solve equations formally, using inverse operations, proved to be difficult for all of the students. The students’ development, in terms of arithmetic to algebraic reasoning, was consistent with Thomas and Tall’s (2001) claim that many students do not achieve the stage of manipulation algebra. Linsell’s study found that the students retained an arithmetic process view of equations in which equations were viewed in terms of the results of substitution into expressions. The students’ application of arithmetic reasoning to solving equations paralleled Herscovics and Linchevski’s description of “students working around the unknown at a purely numerical level” (1994, p. 70). It was apparent that the level of numeracy displayed by the students was a strong predictor of the amount of algebra they would learn during the topic. Furthermore, it appeared to be specifically the students’ understandings of arithmetic structure and inverse operations that were important to their learning to solve equations.
It appears that the part–whole thinking required for algebra poses conceptual difficulties beyond those inherent in arithmetic. Linsell (2005b) argued that multiplicative part–whole thinking must be a prerequisite for solving equations by formal methods if the student is to have an understanding of the process beyond merely following a procedure. Linsell also postulated that algebraic part–whole thinking is a strategy that extends the Number Framework (Ministry of Education, 2003b). This stage is seen as being more advanced than multiplicative part–whole thinking and is a precursor to the stage of treating equations as objects, as described by Sfard & Linchevski (1994). The details of the stage were described as the ability to conceive numbers as being composed of parts determined by the algebraic structure of expressions, even though the value of some of the parts is not initially known.
The links made between numeracy and readiness for learning algebra need to be investigated in a larger cohort. Linsell suggested that only those students who have mastered multiplicative part– whole thinking are capable of solving equations by the formal process of inverse operations. We now have available the diagnostic tool for assessing students’ stage of numeracy (Ministry of Education, 2003a). A next step would be to determine how students’ stages of numeracy had an effect on their learning of algebra. This would require a diagnostic too for assessing algebraic thinking in the domain of solving equations, which would allow a framework for algebraic thinking to be developed.
2. Aims and objectives of the research
The long-term aims of this research are to determine how students’ stages of numeracy effect their learning of algebra and, in particular, how they solve equations. As noted above, in order to investigate this important area of mathematics education, we needed to develop a diagnostic tool for assessing algebraic thinking in the domain of solving equations, and this was the specific objective for this project. This diagnostic interview will be used in our research on algebraic thinking in 2007 and beyond.
It was therefore proposed that a diagnostic interview, similar to that used in numeracy assessment, be developed. The teachers anticipated that the results from this research would not only enhance students’ learning of algebra in their own schools, but would also inform mathematics educators who were extending the implementation of the Number Framework into high schools.
The aim of this research was to make explicit the knowledge and strategic thinking of students as they make the transition from arithmetic to algebra. We hope that this work will eventually lead to a framework for early algebraic thinking. It is anticipated that this will extend the Number Framework beyond the current upper level of advanced proportional thinking.
In the context of this aim, the research questions were:
- What knowledge and strategies do students use to solve equations?
- What diagnostic questioning is appropriate for eliciting the knowledge and strategies used by students?
3. Research design and methods
Overview
This project took place over one year and used an action research model (Carr & Kemmis, 1986; Kemmis & McTaggert, 1988) to develop the diagnostic interview. The teachers’ practical knowledge of schools and students ensured that the diagnostic interview we developed was appropriate for use with Years 7 to 10 students in schools. It was hoped that the project would lead to a second phase, in which the approach used would employ both qualitative and quantitative methods in order to determine the relationships between arithmetic and algebraic thinking, and to develop a framework for algebraic thinking.
Assembling the team
This research study grew out of meetings of an informal mathematics education group led by Derek Holton. Members of the Otago Mathematics Association are strongly represented in this group. There has been long-standing interest among local teachers about the difficulties experienced by students in learning algebra. The concept of a research project was discussed at the annual general meeting of the Otago Mathematics Association and a number of teachers indicated their desire to participate. We then met to formulate an expression of interest. All members of the team are qualified mathematics teachers, four of whom are currently teaching in schools. Four of the team also have experience in research at the masters level or above. All are strongly committed to collaborative partnership and the empowerment of teachers through participation in research and the development of mathematics education. Team members were: Chris Linsell, University of Otago’s College of Education; Jan Savell, Numberworks, Dunedin; Noel Johnston, King’s High School; Melissa Bell, John McGlashan College; Eric McAuslan, King’s High School; and John Bell, Otago Boys’ High School.
Literature review and discussions
Initially, the teachers needed to become familiar with the research literature on the learning of algebra, in particular the conceptual obstacles, (Booth, 1988) process–object duality (Sfard, 1991), and the transition from arithmetic to algebraic thinking (Thomas & Tall, 2001; Warren, 2003). To achieve this, we held weekly after-school meetings to discuss a small number of research papers. The teachers were then in a position to make significant contributions to the development of the diagnostic interview questions.
Writing questions for the diagnostic interview
Initially the teachers and lead researcher made use of current research literature to conjecture the various strategies that students might use. We then collaboratively wrote questions designed to reveal these strategies.
Trialling the questions with students
Students from the teachers’ own schools were used for trialling the questions in the development process of the diagnostic interview. Recorded interviews of students were analysed by the whole research team. The teachers had access to students in their own classes plus other Years 7 to 10 students at their schools.
Reviewing, rewriting questions, and retrialling
An iterative action-research process was used to develop the diagnostic interview. Each teacher used the questions with students, recording the interviews on videotape. We had regular meetings of the research group to view the videotapes and discuss the effectiveness of the questions and the students’ strategies that were revealed. Some questions were ineffective or redundant, while alternative strategies required further questions in order to identify them clearly. Questions were rewritten in order to refine the diagnosis. This process was iterated four times during the year.
Finalising the diagnostic interview
In the last iteration, we reflected on what we had learnt in previous drafts of the diagnostic interview and wrote an assessment that we could use in the future. By the end of 2006, we had a diagnostic interview capable of revealing the knowledge and strategies that students use to solve linear equations. We also had data on the knowledge and strategies of a small number of students.
Ethical considerations
The project was presented to the principals of each school involved before work began. Ethical approval was obtained from the Dunedin College of Education’s Research Ethics Committee (who met on 3 May 2006). There were no difficulties with ethical considerations as the information being collected by the teachers was useful diagnostic assessment information that informed their own subsequent teaching of the students, and was good quality practice in the schools. We then sent letters to each principal, seeking permission to send information letters and consent forms to parents of selected students. All principals gave permission and the teachers gave out the information letters and consent forms. The information letters and consent forms ensured that students, parents, and caregivers were happy for the students to be videotaped and interviews with their teachers transcribed (see Appendix A).
Project timetable
The research was conducted over four terms in 2006. For full details of the timetable, refer to Appendix B.
Discussion of research design
There are a number of issues related to the research design that are likely to be of relevance to other researchers. These are discussed below.
Literature review
The first term of the project was spent getting familiar with the research literature. Weekly meetings were held to discuss a couple of papers or chapters from books. This ensured that all team members were fully informed so that they could contribute to the writing of the diagnostic interview. This was clearly time consuming but, we believe, extremely worthwhile. The approach ensured a real partnership between the teachers and the lead researcher, in which the views of everyone were fully respected. In subsequent meetings, there were frequent references to ideas from the literature. The teachers also commented on their perspectives changing as a result of getting to know the literature. This had an effect on classroom practice, including on the teaching of more senior classes.
Meetings
As we were working with secondary teachers, we decided that teacher release days were not useful because of the disruption it would cause to teaching programmes. Our model was to fund the teachers for 0.1 of their salary so that they could have a reduced teaching commitment throughout the year. However, it proved to be impossible to co-ordinate meeting times within the school day. Meetings of up to two hours could be held after school, but for the practical meetings where we were viewing videotapes, we needed longer and therefore scheduled the meetings for Saturdays. In fact, as the project progressed, we found that we needed full days together.
Returning consent forms
It is difficult to ensure that secondary school students bring forms back to school. As we were working on very tight schedules, the shortage of students with signed consent forms was often a limiting factor on who we could interview.
Practicalities of interviews
We learnt a lot about conducting interviews with students and recording these for subsequent viewing. It was useful for everyone to use the same type of digital tape, so that all tapes could be played in the same machine. Digital tape also meant that snippets could be turned into computer files. Coloured question cards were useful for facilitating access to parts of tapes when fast-forwarding. It was also useful to have explicit coding systems for the teachers to use when evaluating the student responses.
4. Findings
Research question 1: What knowledge and strategies do students use to solve equations?
Our initial classification of strategies for solving equations was based on the work of Kieran (1992), whose highly respected review of the learning and teaching of algebra described the strategies that students use. However, we added some further strategies that we had observed students using. We considered an inverse operation (1c) (see Figure 1) on a one-step equation to be different to Kieran’s working backwards (3b) on multi-step equations. It was difficult to distinguish the difference between Kieran’s known basic facts (1a) and inverse operations (1c), as students often justified their answer by describing the inverse operation when, in fact, what they had done was use a known fact. One-step equations with larger numbers were therefore used to elicit the use of inverse operations. We also found that the strategy of working backwards was not as homogeneous as had been assumed. Many students partly worked backwards and then used either known facts (3c) or guess and check (3d). When large or decimal numbers precluded the use of these strategies they could no longer use working backwards. We also included the strategy of using a diagram (5). This resulted from our explorations of questions in context, where a number of students solved equations through direct use of diagrams.
Our final classification of strategies is listed in Figure 1. It should be noted that this is not intended to be hierarchical, as we have insufficient evidence to make such a claim. In fact, 3c and 3d are clearly less sophisticated strategies than 3b and, at present, we do not know the relative sophistication of 5.
Figure 1 Classification of strategies for solving equations
| 0. | Unable to answer question |
| 1a. | Known basic facts |
| 1b. | Counting techniques |
| 1c. | Inverse operation |
| 2. | Guess and check |
| 3a. | Cover up |
| 3b. | Working backwards |
| 3c. | Working backwards then known facts |
| 3d. | Working backwards then guess and check |
| 4. | Formal operations/equation as object |
| 5. | Use a diagram |
(Based on Kieran, 1992; our amendments in italics)
Research question 2: What diagnostic questioning is appropriate for eliciting the knowledge and strategies used by students?
In a manner similar to that used in the numeracy development projects (Ministry of Education, 2003b), we found it useful to separate the questions into knowledge and strategy components (see Appendix C). The initial classification was somewhat arbitrary, but as we refined the diagnostic interview, we focused more on the solving of equations and the prerequisite knowledge for the use of the variety of strategies became clearer. Students’ uses of strategies were assessed by interview, as there was a need for supplementary questions. However, in the later iterations of the diagnostic tool, knowledge was assessed by a written test, guided by the research literature and our own experience. The focus of the strategy interview was on how students solved equations. In order to determine the most sophisticated strategies that students could use, we asked a series of increasingly complex questions. Our conjecture, that the full range of strategies could be elicited from students without using all the permutations of linear equations suggested by Herscovics and Linchevski (1994), appeared to be correct. Many students successfully solved the easier equations, and they used a broad range of strategies to solve them. In contrast, few students successfully solved our more difficult equations and only a small number of more sophisticated strategies were employed. Students were expected to attempt to solve these equations and explain their strategies. The students were given access to calculators and pencil and paper, but they did not have to use them. The teachers recorded the students’ solutions and classified the strategies used. Initially we were not clear whether questions that were in context or purely abstract would elicit the most sophisticated strategies, and we used a mixture of the two. However, we found that many students performed significantly better on questions that were in context and, therefore, for the later versions of the interview, we produced parallel questions—in context and abstract, as in examples a and b:
| Example a: | In the equation 3n – 8 = 19, what does n stand for? |
| Example b: | Here are 3 packets of beans, that started with the same number in each packet, but a mouse ate 5 of the beans. There are now 16 beans left in the packets, like this pile over here. How many were in each packet at the beginning? |
Our knowledge questions focused on knowledge not routinely assessed in numeracy evaluations (Ministry of Education, 2003a). The knowledge we were assessing was:
- using symbols and letters to represent an unknown
- manipulating symbols/unknowns (lack of closure)
- forming expressions with unknowns/symbols in them
- understanding of the equals sign
- operations on integers y understanding of arithmetic structure
- understanding of inverse operations.
While it is debatable as to what constitutes knowledge and what constitutes strategic thinking, we considered these attributes to be required knowledge for students to use some the previously listed strategies. Examples of the questions we used for understanding of arithmetic structure are:
What answer do you get for each of the following?
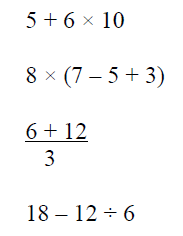
To summarise, we believe that the diagnostic interview we have developed is a useful tool for investigating the strategies used by students to solve equations. The knowledge section of the assessment, however, certainly does not give us complete information about the knowledge required by students to use these strategies. The most important reason for this is that we did not attempt to investigate all prerequisite knowledge, as much of this is routinely assessed using the numeracy development project diagnostic assessments. Knowledge of multiplication facts, for example, is clearly prerequisite knowledge for using inverse operations. Whether our knowledge section gave complete information on the additional knowledge required is not yet clear. A much larger cohort of students needs to be investigated to give us data suitable for statistical analysis.
Strategic value
Understanding the processes of teaching and learning
The main strategic focus of this project was to build understanding of the learning of algebra. Algebra is not easily understood by many students (Brekke, 2001; Cockcroft, 1982; Freudenthal, 1973; Hewitt, 2001). As Bednarz (2001) says:
Even though an abundant corpus of research already exists on the subject, the teaching of algebra, particularly during the initial stages when students construct a certain relationship to this new knowledge, remains a central issue in mathematics teaching. Within this problematic [sic], the question of the transition from arithmetic to algebra is of central concern. (p. 69)
Irwin and Britt (2005) are investigating the effect that numeracy development project instruction has on children’s use of quasi-variables, and our project has complemented their work by focusing on the solving of equations. Linsell (2005a) has argued that some strategies for solving linear equations are essentially arithmetic while the more sophisticated strategies involve algebraic thinking. While the transition from arithmetic to algebraic reasoning has been identified as being of great importance (Bednarz, 2001; Warren, 2003), the way in which this transition occurs is poorly understood. The findings of Linsell’s (2005a) study suggest explicit links between solving equations and numeracy. Our current study has provided a diagnostic tool for investigating this further. Furthermore, we have identified a finer grain in the strategies that students employ than has previously been suggested. Of particular interest for further study is the way in which the strategy of working backwards is developed. Our finding, that this is not a homogeneous strategy, offers opportunities for teachers to provide focused intervention to assist students in developing the strategy.
Addressing diversity
Current approaches to teaching algebra are not successful with many students (Brekke, 2001), with the result that many students do not have the prerequisite skills for participation in higher education. The development of a diagnostic interview for algebraic reasoning has improved the possibility of these students gaining success. If teachers understand the strategies that students use and the prerequisite numeracy skills for algebra, they will then be better placed to provide appropriate learning experiences to facilitate the students’ development of algebraic thinking.
Exploring future possibilities
We hope that this study will lead to an extension of the Number Framework (Ministry of Education, 2003b) into early algebra. New Zealand is a leading country in the development of approaches to numeracy, and is implementing a number of major initiatives under the umbrella of the numeracy projects. The diagnostic interview that has been developed in this project will be useful to the intended extensions of the Number Framework. The Ministry of Education hopes to develop an algebra framework that will follow a similar path to that used for the Number Framework, which started with a focus on the domain of addition and subtraction. We view our work as being within one domain of algebra—the domain of solving equations. Other domains might be generalised numbers and relational thinking. The numeracy projects have been highly successful in improving the outcomes in arithmetic for students through professional development of teachers (Higgins, 2003; Irwin, 2003; Thomas, Tagg, & Ward, 2003). A framework for early algebra has the potential to similarly improve the outcomes for high school students.
Practice value
Likely effect on practice
This project has provided the teachers involved with the opportunity to examine and develop their ideas on teaching numeracy in a “learning community”. Participation in such a community provides ongoing support for changes in teacher beliefs and therefore teaching practice (Cobb, McClain, Lamberg, & Dean, 2003; Franke & Kazemei, 2001). Teacher comments (as noted in the milestone reports) indicate this. Close attention to assessment data and growing familiarity with a hierarchy of student strategies has also proved effective in changing teacher beliefs (Fennema, Carpenter, Franke, Levi, Jacobs, & Empson, 1996; Franke, Carpenter, Fennema, Ansell, & Behrend, 1998; Steinberg, Empson, & Carpenter, 2004). The familiarity with the research literature and potential for conceptual change, ignited by close observation of the students involved, has ensured that the teachers have examined and improved their own teaching practice.
This is illustrated in the following accounts by three of the teachers.
Teacher 1
I have always taught this topic formally, and approached it from some different angles. The traditional progression of collect like terms, expand and factorise, and solve has been the usual method, fraught with the frustration that you know most of the class is not always with you. I have dabbled with approaching the topic through patterns, but not found this particularly successful. I have been looking for some way of getting pupils to understand this topic, and make it as accessible and relevant as number, but always falling short. Contrived “problems” seem to make heavy weather of this topic for most, too. Parents have long been aware, for the most part, that algebra is extremely difficult and give tacit approval that it is OK to not succeed at algebra, because they could never do it either! Ideally, I would like all pupils to be able to solve two-step equations at Year 9, and three-step by Year 10, but this is an aim rather than a realistic expectation for the cohort. I am acutely aware that not all pupils are at the same stage in the Number Framework in Year 9, and this inhibits pupils in their learning of algebra.
After having read a number of academic articles on the teaching and learning of algebra, I am now aware that treating an equation as an object to be manipulated is not a simple concept. Neither is the reading of an equals sign to signify equivalence easily comprehended. Many pupils understand it to mean “compute now”! This is quite a revelation for me and my teaching—that the pupils do not actually read the equation the same as I do! Also the number of pupils who do not see 3n as 3 times n, rather as thirty-something was disturbing. I clearly presumed far too much in my teaching of this strand.
This project has already impacted on my teaching. I have even gone through the treating of an equation as an object with my Year 12 class, and found some misconceptions there that I would not have found otherwise. I have also caught myself presuming pupils at Year 10 know how to treat an equation as an object, as well as assuming they read an equation the same way I do.
I see a better progression for the teaching of solving equations as being:
-
- solving simple problems in context
- writing contextual problems in formal algebraic sentences
- solving equations by formal methods.
This is how I will approach this unit next year. I suspect I will not get it right the first time, but certainly I feel I’ll have a much better chance of engaging the pupils in the learning of algebra.
My involvement in the project has given me a sense of inadequacy, in terms of what I need to know in order to make algebra (and the solving of equations in particular) more accessible to my pupils at all levels of the school. I firmly believe that my participation will make me a better teacher, as well as making a framework for the teaching of equation solving. This is the key to unlocking this part of the algebra mystery.
Teacher 2
It is common knowledge that many pupils (13 to 14 years old) are very wary about learning algebra. A fair bit of this concern is inherited from their parents and some from the way that it is introduced to them in primary/intermediate schools. Many are introduced to the concept of variables and unknowns too abruptly and have difficulty trying to understand where they fit into the whole mathematical scheme. If a pupil does not have some fluency with algebraic manipulations, then solving equations is going to be very demanding and will only be mastered by applying some algorithmic method. The readings that I was exposed to in this study did help to highlight the hierarchy of understanding and appreciation of processes that a pupil needs before they can be expected to be able to meaningfully set about working with equations.
I have introduced algebra (with out yet calling it algebra) in a number of ways. These include generalising from looking at: how numbers function using the associative and distributive properties; generalising from patterns (particularly the pyramid-type ones where the lower adjacent numbers are added together to give the one above) and eventually putting in letters; and working from a “flow chart” type layout where initially numbers are cycled through operations and after passing through three or four different operations an answer emerges, with eventually letters being used. I have found that these approaches are good for introducing pupils to working with, and on, unknowns. Eventually I tell them that they have been doing algebra.
For solving equations, I introduce this also with a range of approaches. These include using the “box” method, and using materials and getting pupils to “balance” equations. I am now a lot more aware of what underpins gaining algebra understanding. I also have more ways of teaching that can be effective, especially the role of “materials” in lesson presentation.
Teacher 3
At the start of the project I was very aware of the panic element of algebra. This is partly due to popular media portrayals of algebra being complex and useless, and I always found this was often reinforced by parents of students I taught. I was also aware that students perceived algebra as “new” with no links to other aspects of mathematics. In my teaching I had tried to emphasise the relationships between algebra and other branches of maths and also the usefulness of algebra in maths and everyday life. I was confused about the lack of a clear framework for algebraic thinking and tended to classify this in terms of the complexity of the equations students dealt with rather than the sophistication of the strategies used.
Now I have the beginnings of a framework in my head that looks at how students solve equations. I am far more aware of the misconceptions students have (equals sign confusion especially), and I am more aware of the required knowledge needed. I hope that all of this means a more methodical and careful approach to teaching algebra. Through awareness of the issues students have with algebra, I feel that my teaching is a little less haphazard than in the past.
In the past I have introduced algebra through a pattern approach, using materials to explore patterns and relationships, generalising relationships, and solving equations based on these situations. I still intend to do the same, but will have more recognition of the prerequisite knowledge aspects. I will also make more links to generalising arithmetic relationships with reference to the numeracy framework and the range of strategies that students use. I will maintain the modelling of a range of approaches as I feel strongly that students dislike algebra (more than any other branch of maths), as they perceive it as a series of rules. By encouraging a range of approaches, we foster the confident manipulation of numbers and relationships as we do with numeracy.
At the start of the project, I was teaching the solving of equations through use of box diagrams, working backwards, and guess and check. I will continue to do the same. In many ways my teaching of solving equations has not changed radically. I think we have learnt a great deal about how students think when solving equations, but there is still work to be done looking at what we can do in the classroom to broaden the strategies they use. I do avoid the a = apples, b = bananas approach, and we spend a lot more time talking about the idea of letter variables. I am a lot more critical of the examples in text books as I think they are haphazard and reinforce algorithmic type approaches to algebra. I feel that the box diagram representation is an excellent way of showing comprehension of an algebraic relationship and a method for solving algebraic equations. I think this approach is particularly good for early algebra.
Relevance to practitioners
The numeracy projects have focused on the professional development of teachers in order to improve outcomes for children. By involving teachers in this project right from the beginning, they have undergone significant professional development. The numeracy projects have been an outstandingly successful example of teacher professional development that directly improves outcomes for children. Planned developments from this project have the potential to provide a model for lifting achievement in algebra in a similar way. Not only will the result be a tested and reliable tool, but also a hierarchy of understanding that has been developed by teachers and researchers to a point where it can itself become a useful tool. Many teachers in numeracy schools have seen the difference that the numeracy professional development has made to their students’ achievement in number, and they are hungry to extend those gains to other strands of the mathematics curriculum.
Transfer to the learning environment
The aim of this project was to improve teachers’ understanding of how students solve equations. This knowledge has enabled the teachers to better meet the needs of their students. All the teachers have benefited by a deeper theoretical knowledge of the teaching of algebra. The diagnostic assessment tool is now available for use by the teachers and others involved in the numeracy development projects. Preliminary results from the study have also suggested new approaches to the teaching of algebra, as illustrated in the teachers’ accounts above. None of us had encountered the strategy of cover up (Bednarz et al., 1996) before, but we intend to use it in our teaching.
Potential benefits to students, parents, teachers, and communities
The numeracy projects are having a major impact on the teaching and learning of mathematics in New Zealand Schools (Higgins, 2003; Irwin, 2003; Thomas et al., 2003). By contributing to the extension of these projects it is anticipated that our work will have a significant effect on the teaching and learning of algebra. Until now, within the domain of solving equations, the focus of teachers has been on how hard equations are to solve and whether students solve them successfully. By changing the focus to the strategies that students employ, rather than simply the outcome, we hope for a similar change in approach to the teaching of algebra as has occurred in the teaching of arithmetic.
5. Limitations
This project was always intended as the first stage in developing a framework for algebraic thinking. While we have successfully developed a diagnostic tool, the development of a framework still lies in the future. The diagnostic interview is of limited use unless we have knowledge of a progression of understanding. This can be obtained only by using the diagnostic tool with a cohort of students that is large enough for statistical analysis. The number of students we interviewed during this project is nowhere near large enough for such a purpose. Furthermore, as we were developing the interview during the year, the questions were constantly changing so we did not have consistent data for analysis. However, it is planned to use the diagnostic tool with a large number of students in 2007 and 2008.
A further limitation, that has already been mentioned, concerns the prerequisite knowledge for solving equations. The knowledge section of the diagnostic tool did not give us complete information about the knowledge required by students to use the strategies that we identified. This was because we did not attempt to investigate all prerequisite knowledge, as much of this is routinely assessed using numeracy development project diagnostic assessments. For example, number word sequences are required for counting strategies, and knowledge of multiplication facts is required for using inverse operations or guess and check. Also, whether the knowledge section of our diagnostic tool gave complete information on the additional knowledge required is not yet clear. Again, a much larger cohort of students needs to be investigated to give us data suitable for statistical analysis.
Building capability and capacity
Funding from the TLRI has enabled our research team to undertake collaborative research in the priority area of extending the numeracy development projects into algebra. The whole team was able to engage with research literature and develop a diagnostic tool for early algebraic thinking. The research project was collaborative in that all those involved had the opportunity to contribute to all phases of the research, including data gathering, data analysis, development of the diagnostic tool, and writing up of the results. The project has strengthened partnerships between the schools, the Dunedin College of Education (now the University of Otago’s College of Education), and the franchise-holder of Numberworks Dunedin.
In 2007, two of the participating teachers from this project are involved in the Secondary Numeracy Project (see, for example, Hannah, Harvey, Higgins, Jackson, Maguire, Neill, Tagg, & Thomas (2006)). Another teacher will continue to lead numeracy within her school, though the school is not officially participating in the numeracy projects. The lead researcher presented the findings from the project at the National Numeracy Facilitators Conference in Auckland (Linsell, 2007), and we will be involving many more teachers in the next phase of the project. This plan has strong support from leaders of the Secondary Numeracy Project. Three of the teachers are keen to be involved in the next phase of the project and are determined to use the diagnostic tool that we have developed.
The project fostered greater research capabilities for all the participants. At the time of writing this report, the participating teachers had been involved in contributing to or co-presenting three conference presentations (see Appendix D). They also contributed to the development of this final report. A teacher who co-presented the paper (Linsell, McAusland, Bell, Savell, & Johnston, 2006) at the New Zealand Association for Education Research conference commented that he had previously been unaware of the research in education relevant to his own practice that is occurring in New Zealand today.
There has been long-standing interest among local teachers about the difficulties experienced by students in learning algebra and four more schools have already expressed interest in being involved in the next phase of the research.
Dunedin is in the fortunate position of having strength and depth in mathematics education. Currently, most research is being produced by Derek Holton, Gill Thomas, Tamsin Meaney, and Chris Linsell. However, another member of the University of Otago’s College of Education’s mathematics department is completing a doctorate and the other members of the department are completing masters degrees. Further students are enrolled for doctorates in mathematics education. Four members of the core team of this project have masters degrees and all have been involved in the numeracy projects. The merger between the University of Otago and Dunedin College of Education has created enhanced conditions for research. It is anticipated that involvement in this project will lead to further developments of research in mathematics education in Otago.
Footnote
- Advanced counting, additive part–whole thinking and multiplicative part–whole thinking are strategy stages of the New Zealand Number Framework (Ministry of Education, 2003b). ↑
References
Bednarz, N. (2001). A problem-solving approach to algebra: Accounting for the reasonings and notations developed by students. In H. Chick, K. Stacey, J. Vincent, & J. Vincent (Eds.), 12th International Commission on Mathematical Instruction (ICMI) Study Conference: The Future of the Teaching and Learning of Algebra (pp. 69–78). Melbourne: University of Melbourne.
Bednarz, N., Kieran, C., & Lee, L. (1996). Approaches to algebra: Perspectives for research and teaching. In N. Bednarz, C. Kieran, & L. Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 3–12). Dordrecht: Kluwer Academic Publishers.
Booker, G. (1987). Conceptual obstacles to the development of algebraic thinking. In J. C. Bergeron, N. Herscovics, & C. Kieran (Eds.), 11th Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 275–281). Montreal, Canada.
Booth, L. (1988). Children’s difficulties in beginning algebra. In A. F. Coxford & A. P. Schulte (Eds.), The ideas of algebra, k-12, 1988 yearbook (pp. 20–32). Reston, VA: National Council of Teachers of Mathematics.
Brekke, G. (2001). School algebra: Primarily manipulations of empty symbols on a piece of paper? In H. Chick, K. Stacey, J. Vincent, & J. Vincent (Eds.), 12th ICMI Study Conference: The Future of the Teaching and Learning of Algebra (pp. 96–102). Melbourne: University of Melbourne.
Carr, W., & Kemmis, S. (1986). Becoming critical: Education, knowledge and action research. London: Falmer Press.
Cobb, P., McClain, K., Lamberg, T., & Dean, C. (2003). Situating teachers’ instructional practices in the institutional setting of the school and district. Educational Researcher, 6, 13–24.
Cockcroft, W. H. (1982). Mathematics counts: Report of the committee of enquiry. London: Her Majesty’s Stationery Office.
Darr, C. (2003). The meaning of “Equals”. set: Research Information for Teachers, 2, 4–7.
Dubinsky, E., & McDonald, M. (2001). APOS: A constructivist theory of learning. In D. Holton (Ed.), The teaching and learning of mathematics at university level: An ICMI study (pp. 275–282). Dordrecht: Kluwer Academic Publishers.
Fairchild, J. (2001). Transition from arithmetic to algebra using two-dimensional representations: A school based research study. Oxford: Centre for Mathematics Education Research.
Fennema, E., Carpenter, T., Franke, M., Levi, L., Jacobs, V., & Empson, S. (1996). Mathematics instruction and teachers’ beliefs: A longitudinal study of using children’s thinking. Journal for Research in Mathematics Education, 27(4), 403–434.
Franke, M., Carpenter, T., Fennema, E., Ansell, E., & Behrend, J. (1998). Understanding teachers’ self-sustaining, generative change in the context of professional development. Teaching and Teacher Education, 14(1), 67–80.
Franke, M., & Kazemei, E. (2001). Teaching as learning within a community of practice: Characterizing generative growth. In T. Woods, B. S. Nelson, & J. Warfield (Eds.), Beyond classic pedagogy: Teaching elementary school mathematics (pp. 47–74). Mahwah, NJ: Lawrence Erlbaum Associates.
Freudenthal, H. (1973). Mathematics as an educational task. Dordrecht: Reidel.
Gray, E. M., & Tall, D. O. (1994). Duality, ambiguity and flexibility: A proceptual view of simple arithmetic. Journal for Research in Mathematics Education, 25(2), 115–141.
Hannah, K., Harvey, R., Higgins, J., Jackson, L., Maguire, T., Neill, A., Tagg, A., & Thomas, G. (2006). Evaluations of the 2005 secondary numeracy pilot project and the CAS pilot project. Wellington: Learning Media.
Herscovics, N., & Linchevski, L. (1994). A cognitive gap between arithmetic and algebra. Educational Studies in Mathematics, 27(1), 59–78.
Hewitt, D. (2001). On learning to adopt formal algebraic notation. In H. Chick, K. Stacey, J. Vincent, & J. Vincent (Eds.), 12th ICMI Study Conference: The Future of the Teaching and Learning of Algebra (pp. 305–312). Melbourne: University of Melbourne.
Higgins, J. (2003). Exploring issues in mathematics education, an evaluation of the advanced numeracy project 2002. Wellington: Learning Media.
Irwin, K. (2002). Interim report to the Ministry of Education on the assessment of the intermediate numeracy project and the numeracy exploratory study for year 9 and 10. Auckland: University of Auckland.
Irwin, K. (2003). Exploring issues in mathematics education, an evaluation of the numeracy project for years 7–10 2002. Wellington: Learning Media.
Irwin, K., & Britt, M. (2005). The algebraic nature of students’ numerical manipulation in the New Zealand numeracy project. Educational Studies in Mathematics, 58, 169–188.
Kemmis, S., & McTaggert, R. (1988). The action research planner (3rd ed.). Geelong, Vic.: Deakin University Press.
Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics, 12(3), 317–326.
Kieran, C. (1992). The learning and teaching of school algebra. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 390–419). New York: MacMillan.
Küchemann, D. (1981). Algebra. In K. Hart (Ed.), Children’s understanding of mathematics: 11–16. London: John Murray.
Linchevski, L. (1995). Algebra with numbers and arithmetic with letters: A definition of pre-algebra. Journal of Mathematical Behavior, 14, 113–120.
Linsell, C. (2005a, September). Arithmetic to algebra. Paper presented at the biennial conference of the New Zealand Association of Mathematics Teachers, Christchurch.
Linsell, C. (2005b). Learning algebra in an activity-based mathematics programme. Unpublished doctoral thesis, University of Otago, Dunedin.
Linsell, C., McAusland, E., Bell, M., Savell, J., & Johnston, N. (2006, December). Using action research to learn about learning algebra. Paper presented at the annual conference of the New Zealand Association for Research in Education (NZARE), Rotorua.
Linsell, C. (2007, February). Solving equations: Students’ algebraic thinking. Paper presented at the National Numeracy Facilitators Conference, Auckland.
MacGregor, M., & Stacey, K. (1997). Students’ understanding of algebraic notation: 11–15. Educational Studies in Mathematics, 33, 1–19.
Ministry of Education. (2003a). The diagnostic interview. Wellington: Author.
Ministry of Education. (2003b). The number framework. Wellington: Author.
Saenz-Ludlow, A., & Walgamuth, C. (1998). Third graders interpretations of equality and the equal symbol. Educational Studies in Mathematics, 35, 153–187.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as two sides of the same coin. Educational Studies in Mathematics, 22, 1–36.
Sfard, A., & Linchevski, L. (1994). The gains and pitfalls of reification: The case of algebra. Educational Studies in Mathematics, 26, 191–228.
Steinberg, R., Empson, S., & Carpenter, T. (2004). Inquiry into children’s mathematical thinking as a means to teacher change. Journal of Mathematics Teacher Education, 7(3), 237–267.
Thomas, G., Tagg, A., & Ward, J. (2003). Exploring issues in mathematics education, an evaluation of the early numeracy project 2002. Wellington: Learning Media.
Thomas, M., & Tall, D. (2001). The long-term cognitive development of symbolic algebra. In H. Chick, K. Stacey, J. Vincent, & J. Vincent (Eds.), 12th ICMI Study Conference: The Future of the Teaching and Learning of Algebra (pp. 590–597). Melbourne: University of Melbourne.
Warren, E. (2003). The role of arithmetic structure in the transition from arithmetic to algebra. Mathematics Education Research Journal, 15(2), 122–137.
Acknowledgements
The research team wish to thank the Teaching and Learning Research Initiative (TLRI) for the opportunity for teachers and researchers to work together to further our understanding of algebraic thinking. We would also like to thank the New Zealand Council for Educational Research (NZCER), which administers the TLRI, and in particular Alex Neill (our research contact), Christina Smits, and Robyn Baker.
Most importantly, we also wish to thank the students who participated in this project and the school principals who supported it.
The appendices for this online version of the report have been removed. However, you can access them here
Bibliography of research outputs to date
Linsell, C. (2007, February). Solving equations: Students’ algebraic thinking. Paper presented at the National Numeracy Conference, Auckland.
Linsell, C., McAusland, E., Bell, M., Savell, J., & Johnston, N. (2006, December). Using action research to learn about learning algebra. Paper presented at the annual conference of the New Zealand Association for Research in Education (NZARE), Rotorua.
McAusland, E., Bell, M., Savell, J., Johnston, N., & Linsell, C. (2006, December). Using action research to learn about learning algebra. Paper presented at the Otago Mathematics Association Mini Conference, Dunedin.



